DiseasyImmunity optimisation

library(diseasy)
#> Loading required package: diseasystore
#> 
#> Attaching package: 'diseasy'
#> The following object is masked from 'package:diseasystore':
#> 
#>     diseasyoption

im <- DiseasyImmunity$new()

Motivation

From our testing, we have learned that our method used to express the waning immunity in a compartmental model¹ is a hard optimisation problem. Depending on the choice of optimisation algorithm, the quality of the approximation will vary wildly as well as the time it takes for the algorithm to converge.

To mitigate this issue, we investigate the effect of several optimisation algorithms to identify the best performing one, evaluating both run time and approximation accuracy of the waning immunity target.

?DiseasyImmunity can internally employ the optimisation algorithms of stats, nloptr and optimx::optimr(), which means that we have around 30 different algorithms to test.

Note that the nature of the optimisation problem also changes dependent on the method used to approximate (i.e. “free_delta”, “free_gamma”, “all_free” - see ?DiseasyImmunity documentation), which means that the algorithm that performs well for one method will not necessarily perform well on the other methods.

Setup

Since we are searching for a “general” best choice of optimisation algorithm, we will define a setup that tests a wide range of waning immunity targets.

We define a “family” of functions to test the optimisation algorithms against. These start at 1 and go to 0 within a time scale, $\tau$.

These targets are:

Function	Functional form
Exponential	$\exp\left(-t / \tau\right)$
Sigmoidal	$\exp\left(-(t - \tau) / 6)\; /\; (1 + \exp\!\!(-(t - \tau) / 6)\right)$
Sum of exponentials	$\frac{\exp(-0.5 t / \tau) + \exp(-2 t / \tau)}{2}$

We then construct more target functions from this family of functions:

• The unaltered functions ($f(t)$)
• The functions but with non-zero asymptote ($g(t) = 0.8 \cdot f(t) + 0.2$)
• The functions but with longer time scales ($h(t) = f(t / 2)$)

The optimisation

As stated above, the optimisation algorithms vary wildly in the time it takes to complete the optimisation. To conduct this test in a reasonable time frame (and to determine algorithms that are reasonably efficient), we setup a testing schema consisting of a number of “rounds” where we incrementally increase the number of compartments in the problem (and thereby the number of degrees of freedom to optimise).

In addition, we allocate a time limit to each algorithm in each round. If the execution time exceeds this time limit, the algorithm is “eliminated” and no more computation is done for that algorithm. Furthermore, if the value (error) of the objective function for the optimiser is equal or greater than 1e3 it is also “eliminated”. Note that this is done on per-method basis as we know the optimisation algorithms fare differently for the different methods for approximation.

Once the round is complete, we update the list of eliminated algorithms and then we run the optimisation of $M + 1$ with the reduced set of algorithms.

The entire optimisation process is run both without penalty (monotonous = 0 and individual_level = 0) and with a penalty (monotonous = 1 and individual_level = 1), see vignette("diseasy-immunity") for monotonous and individual_level definitions.

The results of the optimisation round are stored in the ?diseasy_immunity_optimiser_results data-set.

results <- diseasy_immunity_optimiser_results

results
#> # A tibble: 20,816 × 10
#>    target  variation          method strategy penalty     M value execution_time
#>    <chr>   <chr>              <chr>  <chr>    <lgl>   <int> <dbl>          <dbl>
#>  1 exp_sum Base               all_f… combina… FALSE       2 0.420          0.847
#>  2 exp_sum Base               all_f… naive    FALSE       2 0.420          0.715
#>  3 exp_sum Base               all_f… recursi… FALSE       2 0.420          0.651
#>  4 exp_sum Base               free_… naive    FALSE       2 0.420          0.671
#>  5 exp_sum Base               free_… recursi… FALSE       2 0.420          0.702
#>  6 exp_sum Non-zero asymptote all_f… combina… FALSE       2 0.336          0.875
#>  7 exp_sum Non-zero asymptote all_f… naive    FALSE       2 0.336          0.665
#>  8 exp_sum Non-zero asymptote all_f… recursi… FALSE       2 0.336          0.695
#>  9 exp_sum Non-zero asymptote free_… naive    FALSE       2 0.336          0.671
#> 10 exp_sum Non-zero asymptote free_… recursi… FALSE       2 0.336          0.662
#> # ℹ 20,806 more rows
#> # ℹ 2 more variables: optim_method <chr>, target_label <chr>

Global results

To get an overview of the best performing optimisers, we present an aggregated view of the results in the table below. Here we present the top 5 “best” optimiser/strategy combination for each method and penalty setting. To define what it means to be the “best” we simply take the total integral difference between the approximation and the target function across all target functions and problem sizes ($M$).

In addition, we only consider problems up to size $M = 5$ for the general results.

Table 1: Global results (excluding heaviside and linear targets)

penalty	free_delta			free_gamma			all_free
	strategy	optimiser	value	strategy	optimiser	value	strategy	optimiser	value
no	recursive	auglag_slsqp	14.46	recursive	subplex	11.62	naive	auglag_slsqp	10.41
no	recursive	bfgs	14.46	recursive	neldermead	12.12	naive	slsqp	10.41
no	recursive	bobyqa	14.46	naive	uobyqa	12.15	naive	tnewton	10.41
no	recursive	ccsaq	14.46	recursive	nmkb	12.19	naive	ucminf	10.41
no	recursive	cg	14.46	naive	lbfgs	12.46	naive	uobyqa	10.41
yes	naive	auglag_slsqp	15.80	recursive	hjkb	13.84	combination	neldermead	11.51
yes	recursive	auglag_slsqp	15.80	naive	hjkb	14.00	naive	anms	11.62
yes	naive	bfgs	15.80	recursive	neldermead	14.41	combination	anms	11.63
yes	recursive	bfgs	15.80	naive	pracmanm	14.70	combination	slsqp	11.63
yes	recursive	ccsaq	15.80	naive	bfgs	14.86	naive	ucminf	11.63
auglag_lbfgs: auglag with SLSQP as local solver.

To better choose the default optimisers for DiseasyImmunity, we will also consider how fast the different optimisation methods are. For that purpose, we have also measured the time to run the optimisation for each problem.

# Define the defaults for DiseasyImmunity
chosen_defaults <- tibble::tibble(
  "method" = character(0),
  "penalty" = character(0),
  "strategy" = character(0),
  "optim_method" = character(0)
) |>
  tibble::add_row(
    "method" = "free_delta", "penalty" = "no",
    "strategy" = "naive",
    "optim_method" = "ucminf"
  ) |>
  tibble::add_row(
    "method" = "free_delta", "penalty" = "yes",
    "strategy" = "naive",
    "optim_method" = "ucminf"
  ) |>
  tibble::add_row(
    "method" = "free_gamma", "penalty" = "no",
    "strategy" = "naive",
    "optim_method" = "subplex"
  ) |>
  tibble::add_row(
    "method" = "free_gamma", "penalty" = "yes",
    "strategy" = "naive",
    "optim_method" = "hjkb"
  ) |>
  tibble::add_row(
    "method" = "all_free", "penalty" = "no",
    "strategy" = "naive",
    "optim_method" = "ucminf"
  ) |>
  tibble::add_row(
    "method" = "all_free", "penalty" = "yes",
    "strategy" = "naive",
    "optim_method" = "ucminf"
  )

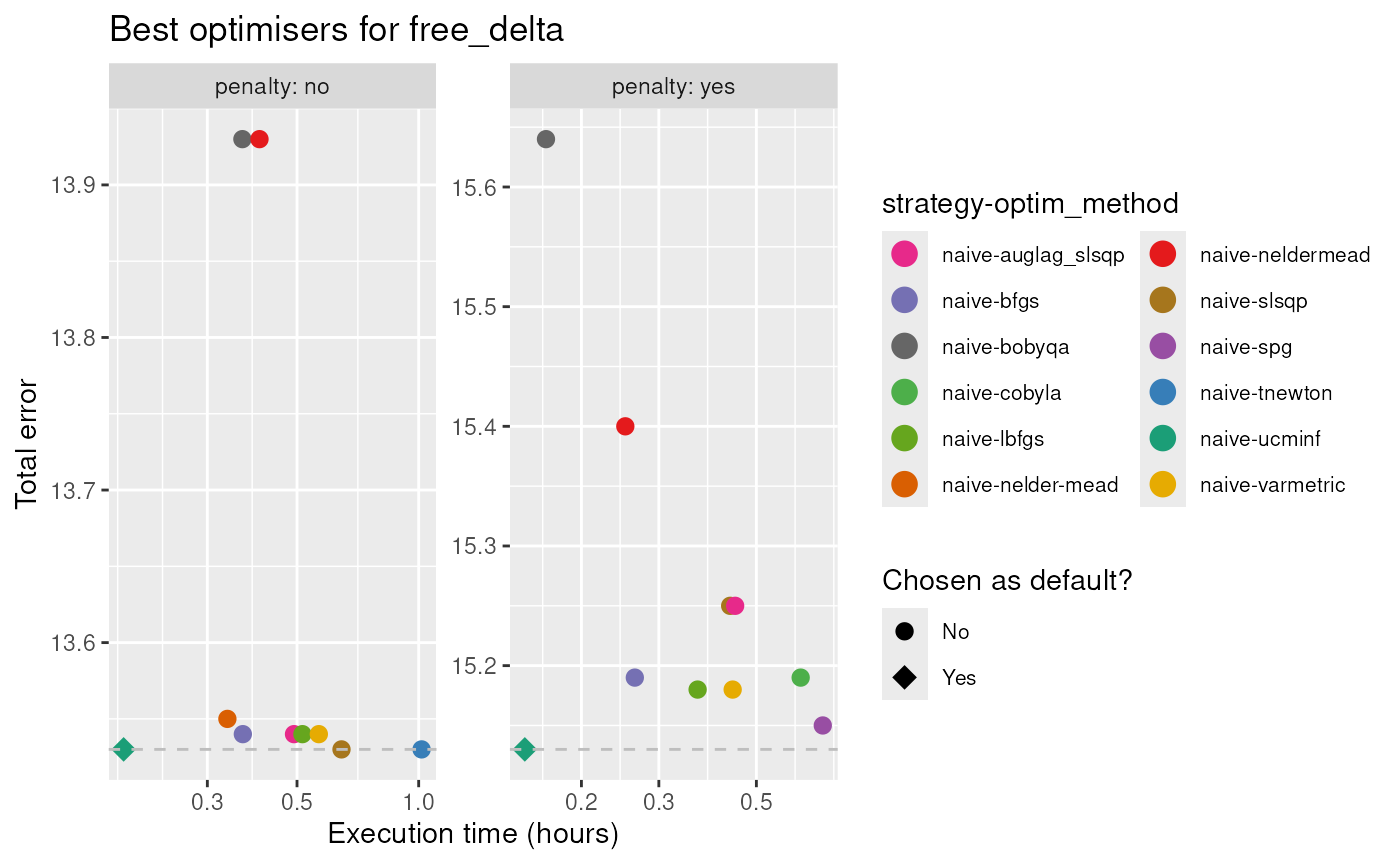
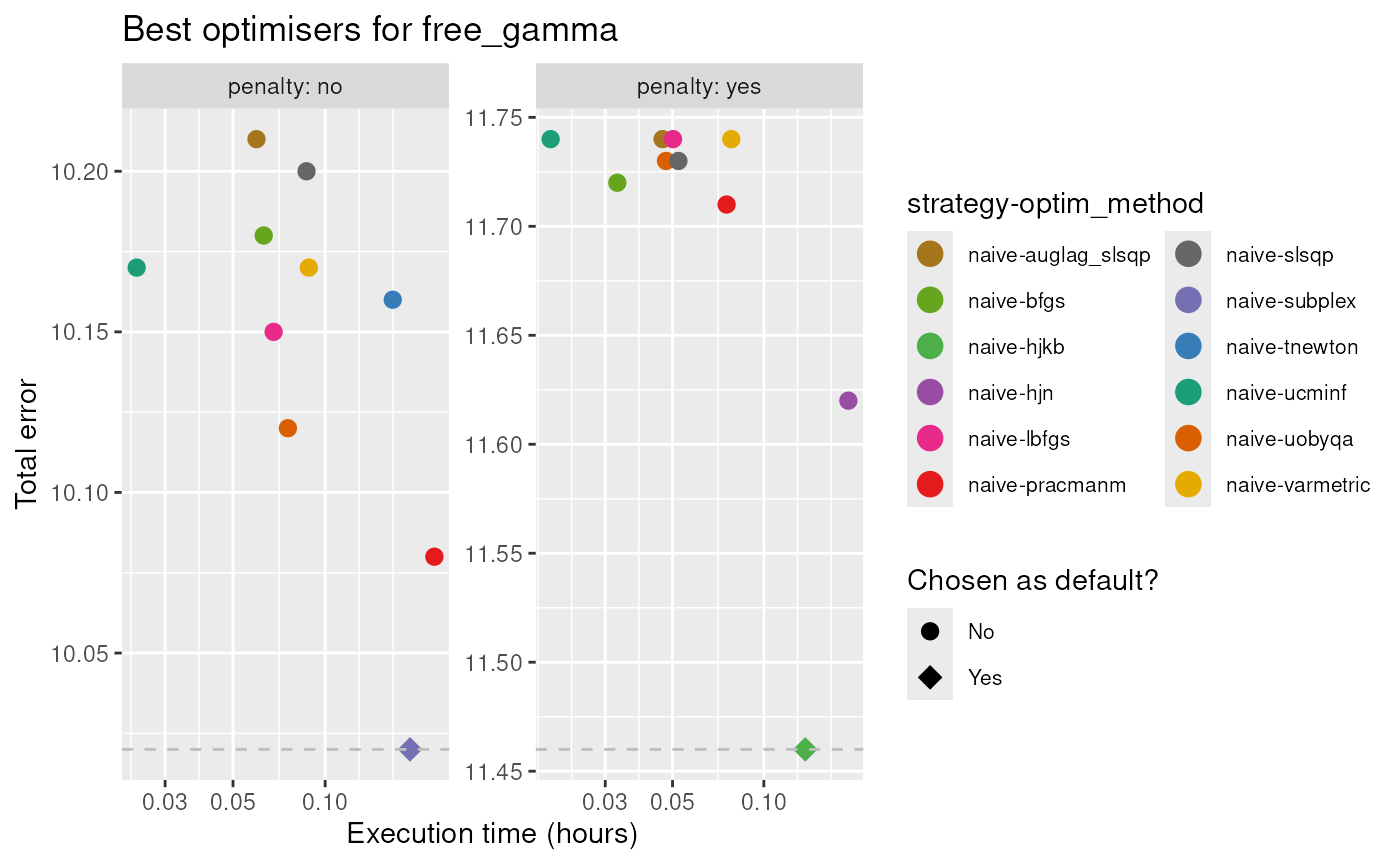
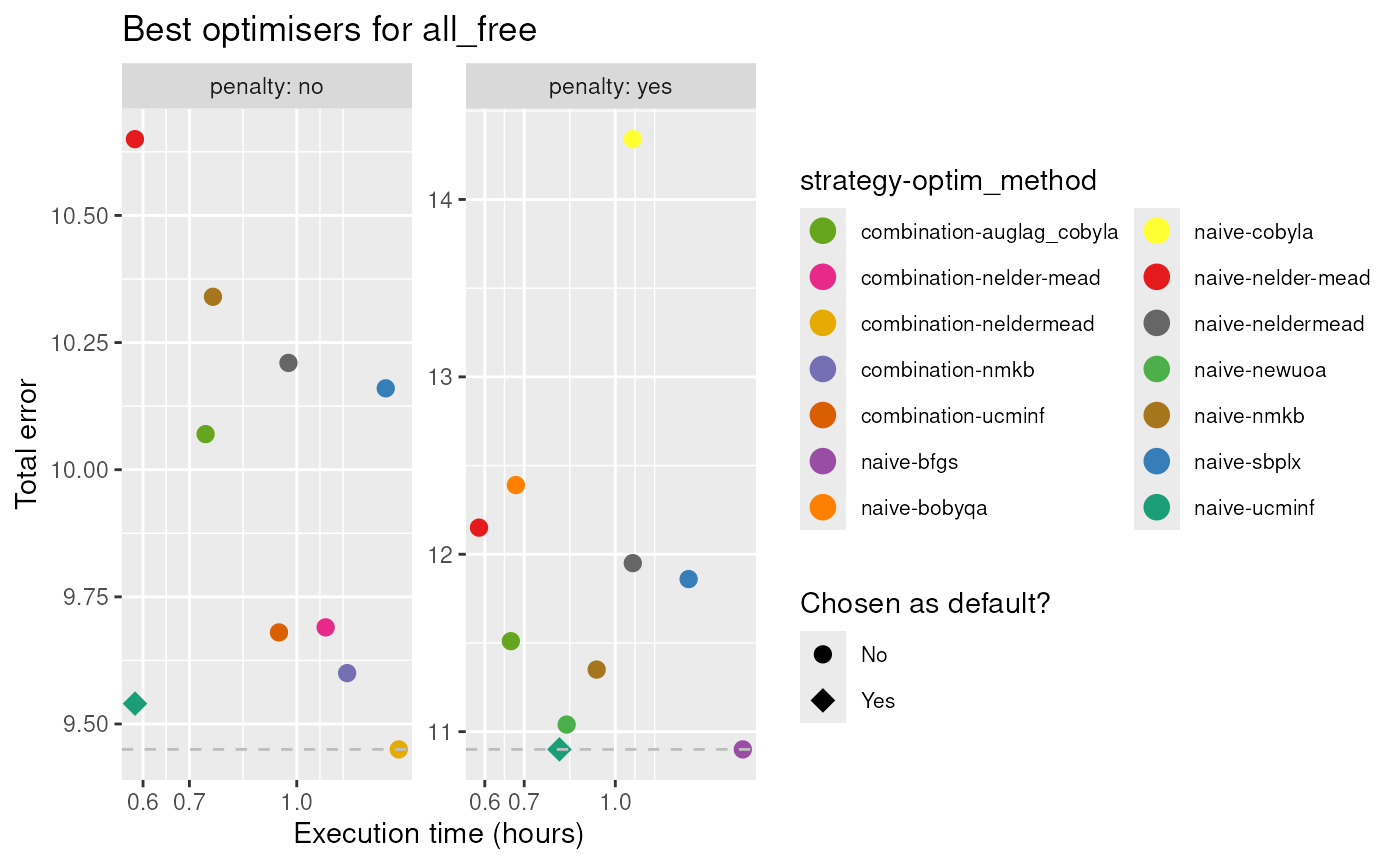
In total, we find that there is no clear choice for best, general optimiser/strategy combination.

For the defaults, we have chose the optimiser/strategy combination dependent on the method of parametrisation and the inclusion of penalty.

The following optimiser/strategy combinations acts as defaults for the ?DiseasyImmunity class:

method	penalty	strategy	optim_method
free_delta	no	naive	ucminf
free_delta	yes	naive	ucminf
free_gamma	no	naive	subplex
free_gamma	yes	naive	hjkb
all_free	no	naive	ucminf
all_free	yes	naive	ucminf

However, as we see in the Per target results section below, the choice of optimiser/strategy can be improved when accounting for the specific target function.

Per target results

Here we dive deeper into the performance of the optimisers on a per target basis. As before, we present best performing optimisers for the given targets in an aggregated view.

We present the top 3 best optimiser/strategy combination for each method and penalty setting.

Table 2: Results for Exponential target

penalty	free_delta			free_gamma			all_free
	strategy	optimiser	value	strategy	optimiser	value	strategy	optimiser	value
no	naive	ucminf	0.00	naive	ucminf	0.00	naive	ucminf	0.00
no	recursive	bobyqa	0.00	recursive	ucminf	0.00	naive	neldermead	0.00
no	recursive	ucminf	0.00	naive	neldermead	0.00	naive	bobyqa	0.00
yes	naive	ucminf	0.37	naive	hjkb	0.31	naive	anms	0.18
yes	naive	neldermead	0.37	recursive	hjkb	0.31	naive	auglag_slsqp	0.19
yes	recursive	bobyqa	0.37	naive	neldermead	0.32	naive	slsqp	0.19
auglag_lbfgs: auglag with SLSQP as local solver.

Table 3: Results for Sum of exponentials target

penalty	free_delta			free_gamma			all_free
	strategy	optimiser	value	strategy	optimiser	value	strategy	optimiser	value
no	recursive	ucminf	1.63	recursive	subplex	2.56	recursive	neldermead	1.24
no	recursive	bobyqa	1.63	recursive	sbplx	2.78	naive	ucminf	1.35
no	recursive	bfgs	1.63	naive	subplex	2.94	naive	bobyqa	1.35
yes	naive	ucminf	2.26	recursive	pracmanm	3.62	combination	pracmanm	1.53
yes	recursive	ucminf	2.26	recursive	hjkb	3.77	combination	neldermead	1.55
yes	naive	bfgs	2.26	naive	hjkb	3.94	naive	pracmanm	1.61

Table 4: Results for Sigmoidal target

penalty	free_delta			free_gamma			all_free
	strategy	optimiser	value	strategy	optimiser	value	strategy	optimiser	value
no	naive	ucminf	12.83	naive	auglag_lbfgs	9.06	naive	ucminf	9.06
no	naive	bobyqa	12.83	naive	uobyqa	9.06	naive	auglag_slsqp	9.06
no	naive	lbfgs	12.83	naive	lbfgs	9.06	combination	sbplx	9.06
yes	naive	ucminf	13.16	naive	subplex	9.74	naive	anms	9.74
yes	naive	spg	13.16	naive	pracmanm	9.74	combination	bfgs	9.75
yes	naive	bobyqa	13.16	naive	bfgs	9.75	naive	bfgs	9.75
auglag_lbfgs: auglag with LBFGS as local solver.
auglag_lbfgs: auglag with SLSQP as local solver.